MM Algorithm Principles

Dr. Alexander Fisher

Duke University

Overview

Definition

• MM stands for “majorize-minimize” and “minorize-maximize”.

• Key idea: it’s easier to optimize a surrogate function than the true objective.

Let \(f(\theta)\) be a function we wish to maximize. \(g(\theta | \theta_n)\) is a surrogate function for \(f\), anchored at current iterate \(\theta_n\), if

• \(g\) “minorizes” \(f\): \(g(\theta | \theta_n) \leq f(\theta) \ \ \forall \ \theta\)

• \(g(\theta_n | \theta_n) = f(\theta_n)\) (“tangency”).

Equivalently, if we wish to minimize \(f(\theta)\), \(g(\theta | \theta_n)\) is a surrogate function for \(f\), anchored at current iterate \(\theta_n\), if

• \(g\) “majorizes” \(f\): \(g(\theta | \theta_n) \geq f(\theta) \ \ \forall \ \theta\)

• \(g(\theta_n | \theta_n) = f(\theta_n)\) (“tangency”).

Toy (conceptual) example

We wish to minimize \(f(x) = cos(x)\).

We need a surrogate \(g\) that majorizes \(f\).

\[ g(x | x_n) = cos(x_n) - sin(x_n)(x - x_n) + \frac{1}{2}(x - x_n)^2 \]

We can minimize \(g\) easily, \(\frac{d}{dx}g(x | x_n) = -sin(x_n) + (x - x_n)\).

Next, set equal to zero and set \(x_{n+1} = x\), \(x_{n+1} = x_n + sin(x_n)\).

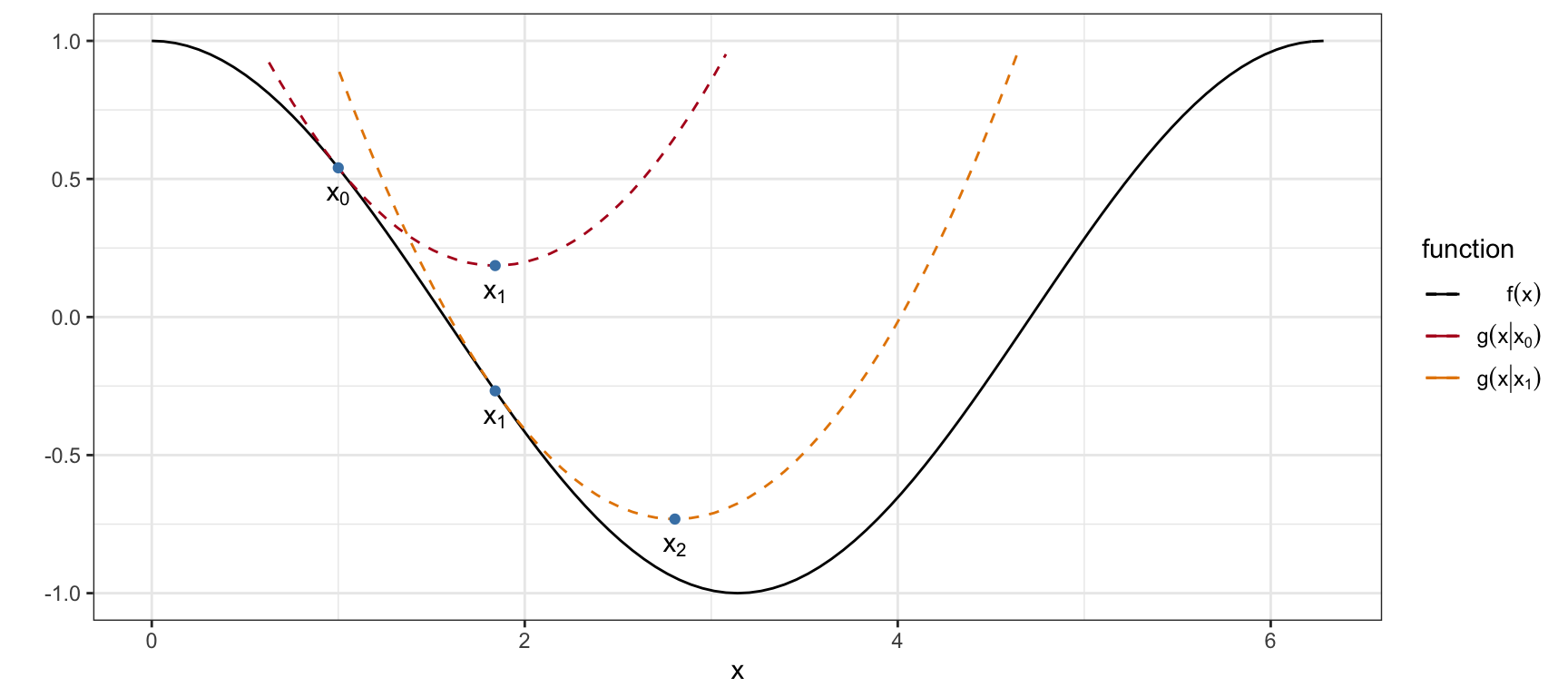
How did we find \(g\)?

Finding \(g\) is an art. Still, there are widely applicable and powerful tools everyone should have in their toolkit.

Toolkit

Quadratic upper bound principle

Objective function: \(f(x)\)

second order Taylor expansion of \(f\) around \(x_n\):

\[ f(x) = f(x_n) + f'(x_n) (x-x_n) + \frac{1}{2} f''(y) (x - x_n)^2 \]

Here, \(y\) lies between \(x\) and \(x_n\). If \(f''(y) \leq B\) where \(B\) is a positive constant, then

\[ g(x|x_n) = f(x_n) + f'(x_n) (x - x_n) + \frac{1}{2} B (x - x_n)^2 \]

This is the “quadratic upper bound”.

Check your understanding

• Questions
• Answers

• does \(g\) satisfy the tangency condition?
• does \(g\) majorize or minorize \(f\)?
• what is \(B\) in the previous (\(f = cos(x)\)) example?
• what is the general update \(x_{n+1} =\) to under the quadratic upper bound principle?

• yes
• majorize
• 1
• \(x_{n+1} = x_n - f'(x_n) / B\)

Convex functions

• A twice-differentiable function is convex iff \(f''(x) \geq 0\). Common examples include \(f(x) = x^2\), \(f(x) = e^x\) and \(f(x) = -\ln(x)\).

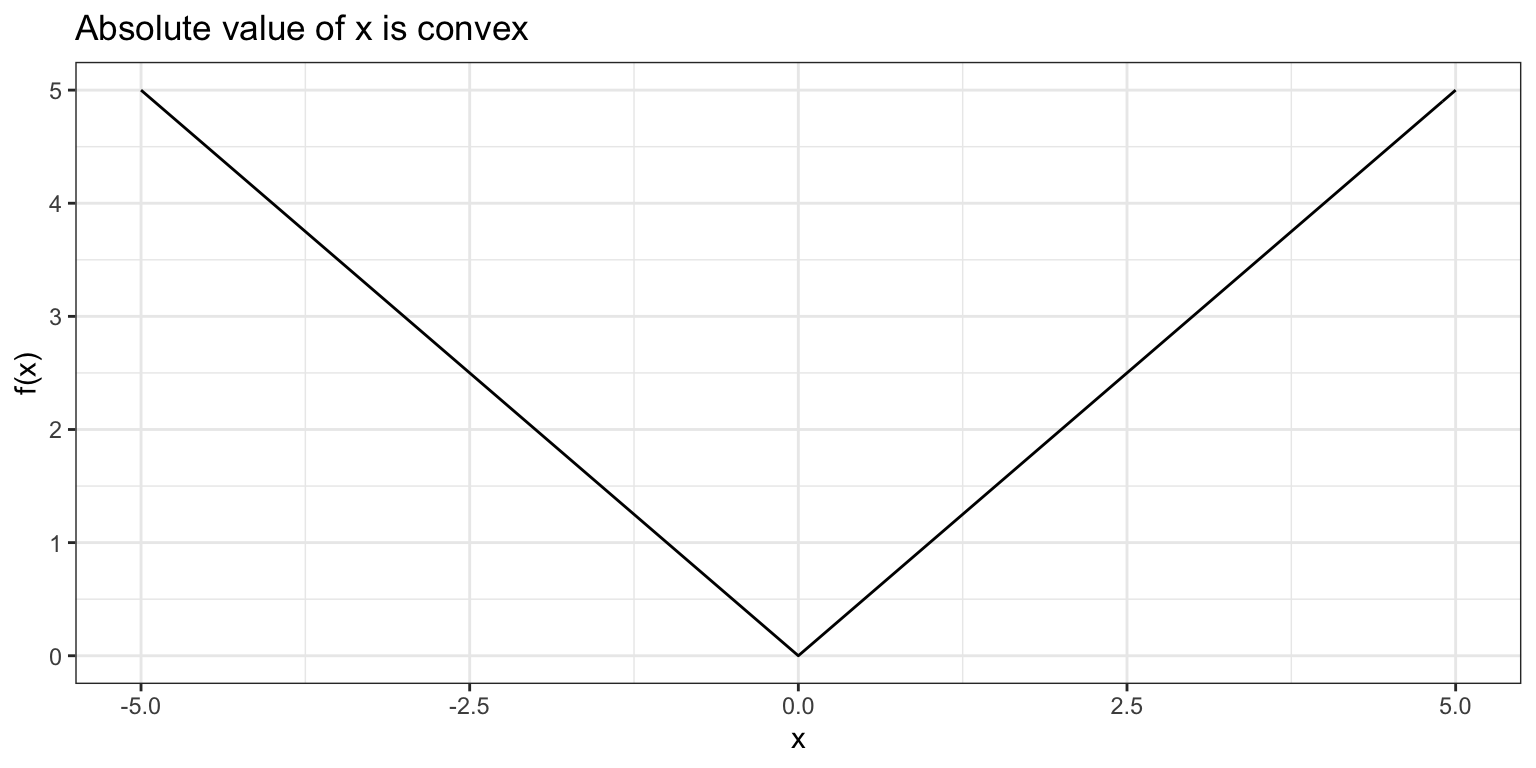
Equivalently, a function is convex if its epigraph (the points in the region above the graph of the function) form a convex set. For example, \(f(x) = |x|\) is convex by the epigraph test.

A function is concave iff its negative is convex.

Supporting line minorization

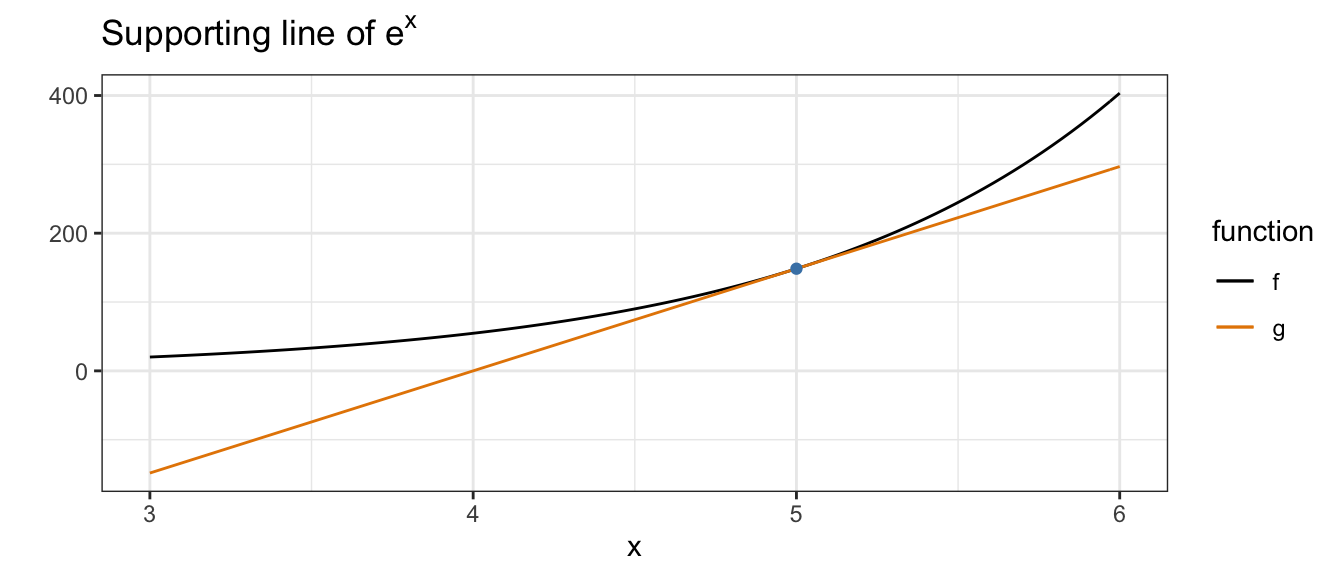
\(f(x) \geq f(x_n) + f'(x_n) (x - x_n)\) because \(f''(x_n) \geq 0\)

Check your understanding

• Write the equation of the line in this example

Jensen’s inequality

For a convex function \(f\), Jensen’s inequality states

\[ f(\alpha x + (1 - \alpha) y) \leq \alpha f(x) + (1-\alpha) f(y), \ \ \alpha \in [0, 1] \]

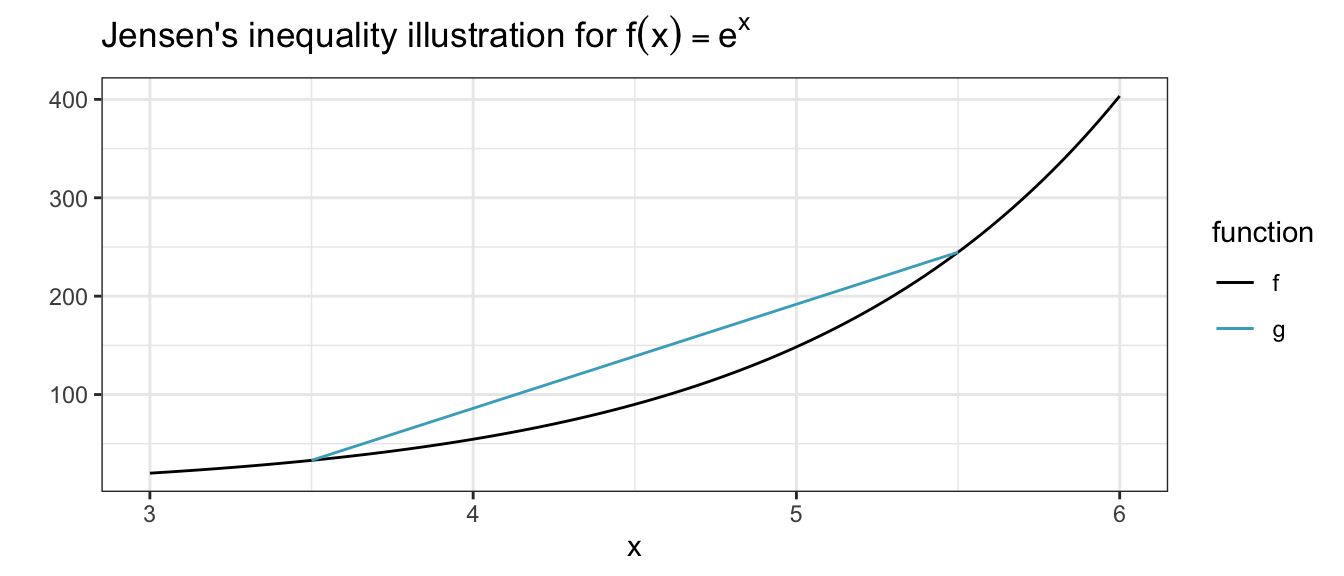
• Big use: majorizing functions of the form \(f(u(x) + v(x))\) where \(u\) and \(v\) are positive functions of parameter \(x\).

\[ f(u + v) \leq \frac{u_n}{u_n + v_n} f\left(\frac{u_n + v_n}{u_n} u\right) + \frac{v_n}{u_n + v_n} f\left(\frac{u_n + v_n}{v_n}v\right) \]

Exercise

part 1

• Using \(f(x) = -\ln(x)\) show that Jensen’s inequality let’s us derive a minorization that splits the log of a sum.

• Note: this minorization will be useful in maximum likelihood estimation under a mixture model

part 2

To see why this will be useful, recall: in a mixture model we have a convex combination of density functions:

\[ h(x | \mathbf{w}, \boldsymbol{\theta}) = \sum_{i = 1}^n w_i~f_i(x | \theta_i). \]

where \(w_i > 0\) and \(\sum_i w_i = 1\).

• Assume you observe \(\{x_1, \ldots x_m\}\) where each \(X_i\) is iid from \(h(\mathbf{x})\). Write down the log-likelihood of the data.

Acknowledgements

Content of this lecture based on chapter 1 of Dr. Ken Lange’s MM Optimization Algorithms.

Lange, Kenneth. MM Optimization Algorithms. Society for Industrial and Applied Mathematics, 2016.